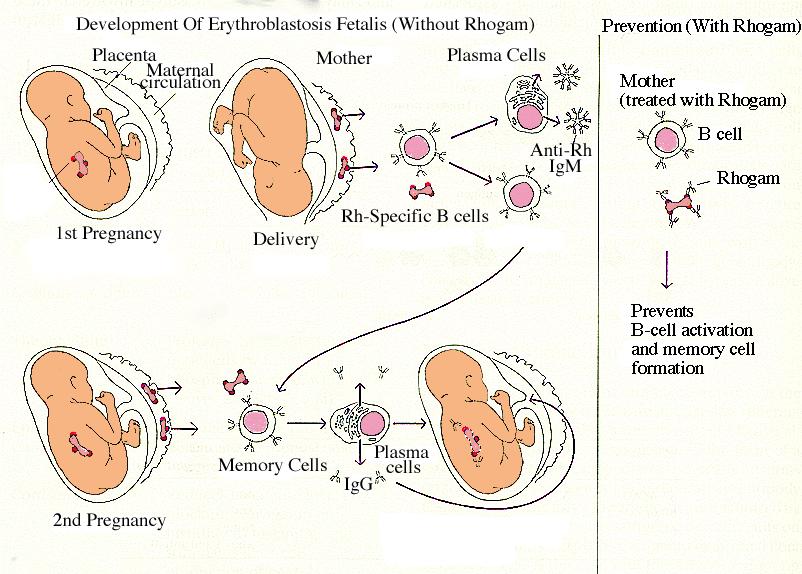
What goes into 36

Teaching Prime Factorization of 36

Number theory—the study of integer numbers—has fascinated mathematicians for years. Fundamental to number theory are whole numbers: 0, 1, 2, 3, and so on. The basic building blocks for all whole numbers are prime numbers. A prime number is a whole number that has only two factors: itself and one. When a number has more than two factors, it is said to be a composite number.

The numbers one and zero are unusual cases. The number one has only one factor and is considered to be neither prime nor composite. The number zero has an infinite number of factors, as zero can be divided evenly by anything except zero. For this reason, zero is also considered neither prime nor composite.

Check Your Understanding:

Is 36 a prime number or composite number? (Composite, because it has many factors other than 1 and 36: 2, 3, 4, 6, 9, 12, and 18.)
What are all of the prime numbers less than 10? (2, 3, 5, and 7. )

Prime Factorization of 36

Students in Grades 4 and up are typically ready to learn about prime factors, and students in Grades 6 and up are typically ready to investigate the prime factorization of a number and explore how it can be used to generate all whole numbers.

Key Standards:

Find factor pairs and recognize that a whole number is a multiple of each of its factors.
Write and evaluate numerical expressions that represent prime factorizations and involve whole-number exponents.

When a composite number is written as a product of all of its prime factors, we have the prime factorization of the number. Thus, if we write 36 as a product of all of its prime factors, we can find the prime factorization of 36.

We can write 36 as a product of prime factors: 36 = 2² × 3². The expression 2² × 3² is said to be the prime factorization of 36.

The Fundamental Theorem of Arithmetic

The Fundamental Theorem of Arithmetic states that every whole number can be factored uniquely (except for the order of the factors) into a product of prime factors. For example, there are many whole numbers that can divide 36: 2, 3, 4, 6, 9, 12, and 18. But no matter which factor you start with, when the number 36 is factored completely, it will always look like 2² × 3². The order in which you factor 36 doesn't matter. Examine the two factor trees of 36 given below.

In the end, it didn't matter if we started factoring 36 using 2 × 18 or 4 × 9. In the end, we still have two factors of 2 and two factors of 3, or altogether, 2² × 3². This would be true if we had started to factor 36 as 12 times 3 or 6 times 6 instead.

Knowing the rules for divisibility will be very helpful when seeking to write a number in prime factorization form. A rule for checking if a number is divisible by two is by seeing if it ends in 0, 2, 4, 6, or 8. Notice that two is the only even prime number.

Dividing by Prime Numbers

Another way to factor a number other than using factor trees is to start dividing by prime numbers, as shown below.

Using this method, the prime factorization is found by looking at all of the numbers outside the division symbols. Once again, we can see that 36 = 2² × 3². Notice the key importance of exponents in writing the prime factorization of a number. An exponent tells how many times the base is used as a factor. In the prime factorization of 36 = 2² × 3², both of the factors 2 and 3 have an exponent of two because each factor appears twice.

It is notoriously difficult to determine whether a number is prime, especially when the number is very large. One useful strategy to check whether a number is prime or not is to only try dividing by prime numbers that, when squared, remain less than the original number. For example, to see if 131 is prime, you need only check for divisibility by 2, 3, 5, 7, and 11, since 13² = 169, and 169 is greater than 131. This strategy works because if 131 were divisible by a prime number greater than 13, then the other factor would have to be less than 13 and you would have already checked it.

***

Looking for comprehensive math instruction for questions beyond "What is the prime factorization of 36?" Explore HMH Into Math, our core math solution for Grades K–8.

Math Activities & Lessons Grades 3-5 Grades 6-8

Related Reading

Brenda Iasevoli
Shaped Executive Editor
February 07, 2023
Alicia Ivory
Shaped Editor
February 03, 2023
Jennifer Corujo
Shaped Editor
January 31, 2023

Factors of 36 | Prime Factorization of 36, Factor Tree of 36

Factors of 36 are those numbers that divide 36 completely without leaving any remainder. There are 9 factors of 36 among which 36 is the biggest factor and 2 and 3 are its prime factors. The prime factorization of 36 can be done by multiplying all its prime factors such that the product is 36. Let us learn about all factors of 36, the prime factorization of 36, and the factor tree of 36 in this article.

1.	What are the Factors of 36?
2.	Prime Factorization of 36
3.	Factor Tree of 36
4.	Factors of 36 in Pairs
5.	FAQs on Factors of 36

What are the Factors of 36?

The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. According to the definition of factors, the factors of 36 are those numbers that divide 36 without leaving any remainder. In other words, we can say if two numbers are multiplied and the product is 36, then the numbers are the factors of 36. It means that 36 is completely divisible by all these numbers. Apart from these, 36 also has negative factors that can be listed as, -1, -2, -3, -4, -6, -9, -12, -18, and -36. For negative factors, we need to multiply a negative factor by a negative factor, like, (-12) × (-3) = 36.

How to Find the Factors of 36?

Factorization of a number means writing the number as a product of its factors. The most commonly used method to find the factors of a number is using the multiplication method. Let us find the factors of 36 using multiplication.

Factors of 36 using Multiplication

Let us find the factors of 36 using the multiplication method using the following steps.

Step 1: In order to find the factors of 36 using multiplication, we need to check what pairs of numbers multiply to get 36, so we need to divide 36 by natural numbers starting from 1 and go on till 9. We need to make a note of those numbers that divide 36 completely.
Step 2: The numbers that completely divide 36 are known as its factors. We write that particular number along with its pair and make a list as shown in the figure given above. As we check and list all the numbers up to 9, we automatically get the other pair factor along with it. For example, starting from 1, we write 1 × 36 = 36, and 2 × 18 = 36 and so on. Here, (1, 36) forms the first pair, (2, 18) forms the second pair and the list goes on as shown. So, as we write 1 as the factor of 36, we get the other factor as 36; and as we write 2 as the factor of 36, we get 18 as the other factor. Like this, we get all the factors.
Step 3: After the list is noted, we get all the factors of 36 starting from 1 up there, coming down and then we go up again up to 36. This gives us a complete list of all the factors of 36 as shown in the figure given above.

Therefore, the factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. Now, let us learn about the prime factorization of 36.

Prime Factorization of 36

Prime factorization is a way of expressing a number as a product of its prime factors. The prime factors of a number are those factors that are prime numbers. The prime factorization of 36 can be done using the following steps. Observe the figure given below to understand the prime factorization of 36.

Step 1: The first step is to divide the number 36 with its smallest prime factor. We know that a prime factor is a prime number which is a factor of the given number. So, with the help of divisibility rules, we find out the smallest factor of the given number. Here, we get 2. Therefore, 2 is the smallest prime factor of 36. So, 36 ÷ 2 = 18
Step 2: We need to repeatedly divide the quotient by 2 until we get a number that is no more divisible by 2. So, we divide 18 again by 2 which is 18 ÷ 2 = 9
Step 3: Divide 18 again by 2 which results in 18 ÷ 2 = 9
Step 4: Now, 9 is not completely divisible by 2, so, we proceed with the next prime factor of 36, which is 3. That is 9 ÷ 3 = 3
Step 5: Divide the quotient by 3 again which is 3 ÷ 3 = 1
Step 6: We need not proceed further as we have obtained 1 as our quotient.
Step 7: Therefore, the prime factorization of 36 is expressed as 2 × 2 × 3 × 3 = 2² × 3²; where 2 and 3 are prime numbers and the prime factors of 36.

Therefore, the prime factors of 36 are 2 and 3 and the Prime factorization of 36 = 2 × 2 × 3 × 3

Factor Tree of 36

We can also find the prime factors of 36 using a factor tree. The factor tree of 36 can be drawn by factorizing 36 until we reach its prime factors. These factors are split and written in the form of the branches of a tree. The final factors are circled and are considered to be the prime factors of the 36. Let us find the prime factors of 36 using the following steps and the factor tree given below.

Step 1: Split 36 into two factors. Let us take 2 and 18.
Step 2: Observe these factors to see if they are prime or not.
Step 3: Since 2 is a prime number we circle it as one of the prime factors of 36. We move on to 18, which is a composite number and further split it into more factors. In other words, we repeat the process of factorizing 18 and splitting it into branches until we reach a prime number.
Step 4: Here, we get 2 and 9. So, we circle 2 because it is a prime number and we split 9 into 3 and 3. At this stage, we are left with prime numbers, 2 and 3. We circle them since we know that they cannot be factorized further. This is the end of the factor tree.
Step 5: Therefore, the prime factors of 36 = 2 × 2 × 3 × 3

Note: It should be noted that there can be different factor trees of 36. For example, we can start by splitting 36 into 4 and 9. Then, 4 can be split further into 2 and 2, while 9 can be split into 3 and 3. Finally, we can observe the same prime factors, that is, 36 = 2 × 2 × 3 × 3

Factors of 36 in Pairs

The factors of 36 can be written in pairs. This means that the product of the pair factors of 36 is always 36.The factors of 36 in pairs can be written as shown in the table given below:

Factors	Positive Pair Factors
1 × 36 = 36	1, 36
2 × 18 = 36	2, 18
3 × 12 = 36	3, 12
4 × 9 = 36	4, 9
6 × 6 = 36	6, 6

It is possible to have negative pair factors as well because the product of two negative numbers also gives a positive number. Let us have a look at the negative pair factors of 36.

Factors	Negative Pair Factors
-1 × -36 = 36	-1, -36
-2 × -18 = 36	-2, -18
-3 × -12 = 36	-3, -12
-4 × -9 = 36	-4, -9
-6 × -6 = 36	-6, -6

The following points explain some features of the pair factors of 36.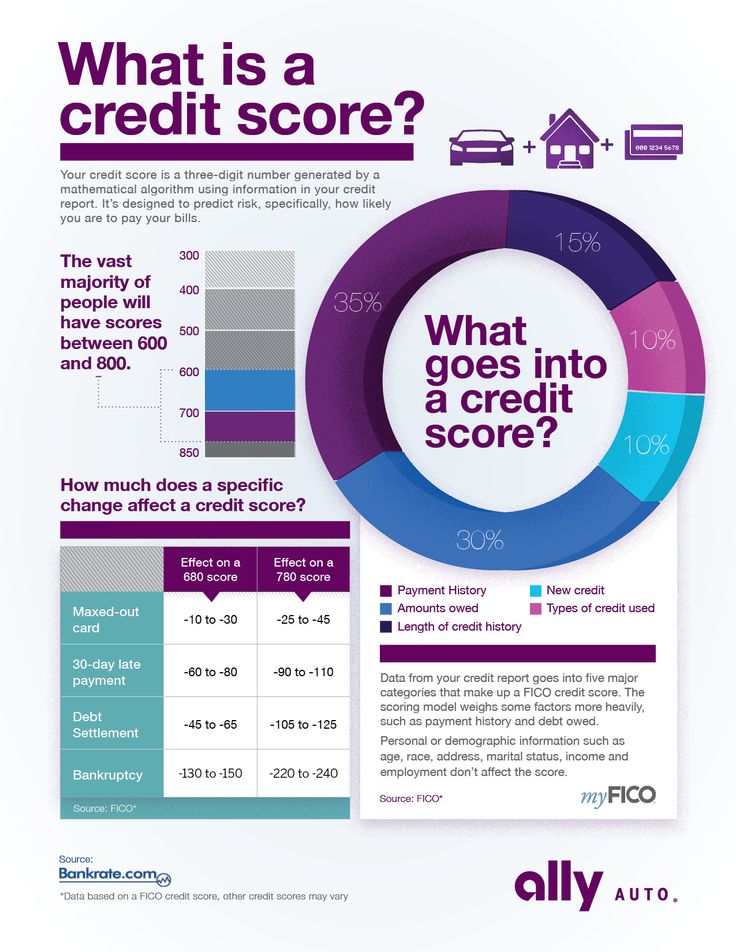

The pair factors of the number 36 are whole numbers in pairs that are multiplied to get the original number, i.e., 36.
Pair factors could be either positive or negative but they cannot be fractions or decimal numbers.
The positive pair factors of 36 are as follows: (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6). The negative pair factors of 36 are (-1, -36), (-2, -18), (-3, -12), (-4, -9) and (-6, -6)

Important Notes

Only composite numbers can have more than two factors. Since 36 is a composite number, it has more than two factors.
Every factor of a given number is either less than or equal to the given number.
The number of factors of a given number is finite. 36 has 9 factors.
Factors of 36 are those numbers that divide 36 completely without leaving any remainder.
36 has a total of 9 factors: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
There is a trick to calculate the total number of factors of a number. For example, 36 = 2 × 2 × 3 × 3 = 2²× 3². We get the prime factorizations of 36 as 2²× 3². Just add one (1) to the exponents 2 and 2 individually and multiply their sums. (2 + 1) × (2 + 1) = 3 × 3 = 9. This means 36 has 9 factors in all.

Points to remember

Let us recollect the list of the factors, the negative factors, and the prime factors of 36.

Factors of 36: 1, 2, 3, 4, 6, 9, 12, 24, and 36.
Negative Factors of 36: -1, -2, -3, -4, -6, -9, -12, -18, and -36.
Prime Factors of 36: 2, 3
Prime Factorization of 36: 2 × 2 × 3 × 3 = 2² × 3²

☛ Related Articles

Factors of 33: The factors of 33 are 1, 3, 11, and 33.
Factors of 34: The factors of 34 are 1, 2, 17, and 34.
Factors of 38: The factors of 38 are 1, 2, 19, and 38.
Factors of 30: The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
Factors of 360: The factors of 360 are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360.
Factors of 35: The factors of 35 are 1, 5, 7, and 35.
Factors of 37: The factors of 37 are 1 and 37.

Examples on Factors of 36

Example 1: State true or false with respect to the factors of 36.
a.) 3 and 6 are factors of 36.
b.) 2 and 3 are the prime factors of 36.
Solution:
a.) True, 3 and 6 are factors of 36.
b.) True, 2 and 3 are the prime factors of 36.
Example 2: Write all the positive factors of 36.
Solution:
All the positive factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Example 3:
List the positive and negative pair factors of 36.
Solution:
The positive pair factors of 36 are as follows: (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6). The negative pair factors of 36 are (-1, -36), (-2, -18), (-3, -12), (-4, -9) and (-6, -6)

go to slidego to slidego to slide

Break down tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Practice Questions on Factors of 36

go to slidego to slide

FAQs on Factors of 36

What are the Factors of 36?

The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36 and its negative factors are -1, -2, -3, -4, -6, -9, -12, -18, -36.

What are the Prime Factors of 36?

There are two prime factors of 36, and they are 2 and 3. The prime factors of a number are those factors that are prime numbers. In this case, if we do the prime factorization of 36, we get 2 × 2 × 3 × 3 = 2²× 3², where 2 and 3 are prime numbers and the prime factors of 36.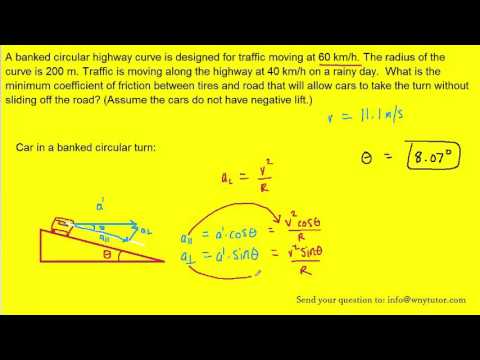

What are the Common Factors of 36 and 42?

The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, 36 and the factors of 42 can be listed as 1, 2, 3, 6, 7, 14, 21, 42. Among these, we can list the common factors of 36 and 42 as 1, 2, 3, and 6. Now, we can find the Greatest Common Factor (GCF) of 36 and 42 which is 6.

What are the Common Factors of 36 and 40?

The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, 36 and the factors of 40 can be listed as 1, 2, 4, 5, 8, 10, 20, 40. Among these, we can list the common factors of 36 and 40 as 1, 2, and 4. With the help of this, we can find the Greatest Common Factor (GCF) of 36 and 40 which is 4.

What is the Greatest Common Factor of 36 and 20?

The factors of 36 and 20 are 1, 2, 3, 4, 6, 9, 12, 18, 36 and 1, 2, 4, 5, 10, 20 respectively. The Common factors of 36 and 20 are (1, 2, 4). Hence, the GCF of 36 and 20 is 4.

What is the Sum of all the Factors of 36?

The sum of all the factors of 36 can be calculated by adding 1, 2, 3, 4, 6, 9, 12, 18, 36 which is 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 + 36 = 91.

Download FREE Study Materials

Factors of 36

Civil Code of the Russian Federation Article 36. Urban Planning Regulations \ ConsultantPlus

Civil Code of the Russian Federation Article 36. Urban Planning Regulations

Prospects and risks of disputes in a court of general jurisdiction. Situations related to Art. 36 of the Civil Code of the Russian Federation

- The administrative plaintiff does not agree with the refusal to change the main type of permitted use of the land plot

and subsequent operation of capital construction projects.

2. Urban planning regulations are established taking into account:

1) the actual use of land plots and capital construction facilities within the boundaries of the territorial zone;

2) the possibility of combining, within the same territorial zone, various types of existing and planned use of land plots and capital construction projects;

3) functional zones and characteristics of their planned development, determined by the documents of territorial planning of municipalities;

4) types of territorial zones;

5) requirements for the protection of cultural heritage sites, as well as specially protected natural areas, other natural objects.

3. The effect of the urban planning regulations applies equally to all land plots and capital construction facilities located within the boundaries of the territorial zone indicated on the urban zoning map.

4. Town planning regulations do not apply to land plots:

1) within the boundaries of the territories of monuments and ensembles included in the unified state register of objects of cultural heritage (monuments of history and culture) of the peoples of the Russian Federation, as well as within the boundaries of the territories of monuments or ensembles that are identified objects of cultural heritage and decisions on the maintenance regime, the parameters of restoration, conservation, reconstruction, repair and adaptation of which are accepted in the manner prescribed by the legislation of the Russian Federation on the protection of cultural heritage sites;

(as amended by Federal Law No. 315-FZ of October 22, 2014)

(see the text in the previous edition)

2) within the boundaries of public areas;

3) intended for placement of linear facilities and (or) occupied by linear facilities;

(clause 3 as amended by Federal Law No. 41-FZ of 20.03.2011)

(see the text in the previous edition)

4) provided for the extraction of minerals.

(Clause 4 was introduced by Federal Law No. 210-FZ of December 31, 2005)

5. In relation to the territories of historical settlements, places of interest, lands of medical and recreational areas and resorts, zones with special conditions for the use of territories, urban planning regulations are established in accordance with the legislation of the Russian Federation.

6. Urban planning regulations are not established for forest fund lands, lands covered with surface waters, reserve lands, lands of specially protected natural areas (with the exception of lands of medical and recreational areas and resorts), agricultural lands as part of agricultural land, land plots, located within the boundaries of special economic zones and territories of priority development.

-FZ, dated 14.07.2022 N 271-FZ)

(see the text in the previous edition)

6. 1. Until the establishment of urban planning regulations for land plots included in the boundaries of settlements from the lands of the forest fund (with the exception of forest plots that were provided to citizens or legal entities before January 1, 2016 or on which real estate objects are located, the rights to which arose before January 1 2016, and the permitted use or purpose of which before their inclusion in the boundaries of the settlement was not associated with the use of forests), such land plots are used subject to the restrictions established for the use of urban forests in accordance with forest legislation.

(Part 6.1 was introduced by Federal Law No. 280-FZ of July 29, 2017)

ConsultantPlus: note.

The permitted use of land plots of a specially protected natural area, which is fully or partially located within the boundaries of the forest fund lands, is established by the regulation on a specially protected natural area (FZ of 03.08.2018 N 342-FZ).

7. The use of land plots that are not covered by town planning regulations or for which town planning regulations are not established is determined by the authorized federal executive bodies, the authorized executive bodies of the subjects of the Russian Federation or the authorized bodies of local self-government in accordance with federal laws. The use of land plots within the boundaries of special economic zones is determined by the governing bodies of special economic zones. The use of lands or land plots from the composition of the lands of the forest fund, lands or land plots located within the boundaries of specially protected natural territories (with the exception of the territories of settlements included in the composition of specially protected natural territories) is determined accordingly by the forestry regulation, the regulation on a specially protected natural territory in accordance with forest legislation, legislation on specially protected natural areas.

(as amended by Federal Laws No. 240-FZ of October 30, 2007, No. 342-FZ of August 3, 2018, and No. 505-FZ of December 30, 2020)

(see the text in the previous version) plots or objects of capital construction, types of permitted use, the limiting (minimum and (or) maximum) sizes and limiting parameters of which do not comply with the town planning regulations, can be used without setting a deadline for bringing them into line with the town planning regulations, except in cases where the use of such land sites and objects of capital construction is dangerous for human life or health, for the environment, cultural heritage sites.

9. Reconstruction of the capital construction objects specified in part 8 of this article can be carried out only by bringing such objects in line with the urban planning regulations or by reducing their non-compliance with the limiting parameters of permitted construction, reconstruction. Changes in the types of permitted use of the said land plots and capital construction facilities may be carried out by bringing them in line with the types of permitted use of land plots and capital construction facilities established by the urban planning regulations.

land plots and objects.

Hyundai Promotion: Free 36 Point Hyundai Diagnosis

All offers

Benefits

Free 36 point diagnostics

Additional free services

No appointment required

Car Care

Best for Your Own Service Program ¹ is a unique offer for owners of Hyundai vehicles older than 2 years. This is a comprehensive care for your car and checking the reliability of its operational properties. How can I take advantage of the Best for Your Own program? Visit a Hyundai service center and use the service of comprehensive free car diagnostics on 36 key points.

Customer care

For your comfort on the road and the convenience of driving, we have expanded the possibilities of the "Best for Your Own" program. Employees of official Hyundai service centers are always ready to help their customers and provide additional types of free services. Pre-registration is not required for work. Works are carried out at the request of the client.

Free services

Comprehensive vehicle diagnostics with 36 key points ³
Battery test
Replacement of external lighting lamps

Replacement wiper blades
Fluid level adjustment
Cabin filter installation

Sign up for a service?

Contact your nearest authorized Hyundai dealer or call customer service 8 800 333-71-67

Make an appointment Service promotions

1 - Only the works specified in the list are free for participants. Consumables and spare parts are subject to payment according to the price list of the dealership. 2 - The list includes only those operations that can be performed in a short period of time and do not require arrival at the service area. The dealer decides on the possibility of performing the operation on a specific car model on his own. The offer is limited, not a public offer, the conditions of the promotion may be changed. You can learn more about the Best for Your Own program from a master consultant at Hyundai official dealerships or on the website www.hyundai.ru. Only individuals can use the services of the Best for Your Own program. The program applies to Hyundai cars sold through official Hyundai dealerships in the Russian Federation; Starex vehicles released for primary circulation in any other market. The following cars do not participate in the program: a.) manufactured by TaGAZ LLC; b.) issued for primary circulation in any other market, including cars from the domestic market of the Republic of Korea (except for Starex cars). 3 - The service of comprehensive free car diagnostics for 36 key points is available only for owners of Hyundai cars older than 2 years. The rest of the services are valid without restrictions for the period of operation of the car.