What does it mean to be in the 90th percentile
Percentiles, Percentile Rank & Percentile Range: Definition & Examples
Statistics Definitions > Percentiles, Percentile Rank & Percentile Range
Contents:
- Percentiles
- Percentile Rank
- How to Find a Percentile
- Percentile Range
1. What are Percentiles?
Watch the video for an overview and a couple of examples:
Percentiles Definition and Examples
Watch this video on YouTube.
Can’t see the video? Click here.
Image: UPRM.edu“Percentile” is in everyday use, but there is no universal definition for it. The most common definition of a percentile is a number where a certain percentage of scores fall below that number. You might know that you scored 67 out of 90 on a test. But that figure has no real meaning unless you know what percentile you fall into. If you know that your score is in the 90th percentile, that means you scored better than 90% of people who took the test.
Percentiles are commonly used to report scores in tests, like the SAT, GRE and LSAT. for example, the 70th percentile on the 2013 GRE was 156. That means if you scored 156 on the exam, your score was better than 70 percent of test takers.
The 25th percentile is also called the first quartile.
The 50th percentile is generally the median (if you’re using the third definition—see below).
The 75th percentile is also called the third quartile.
The difference between the third and first quartiles is the interquartile range.
2. Percentile Rank
The word “percentile” is used informally in the above definition. In common use, the percentile usually indicates that a certain percentage falls below that percentile. For example, if you score in the 25th percentile, then 25% of test takers are below your score. The “25” is called the percentile rank. In statistics, it can get a little more complicated as there are actually three definitions of “percentile. ” Here are the first two (see below for definition 3), based on an arbitrary “25th percentile”:
” Here are the first two (see below for definition 3), based on an arbitrary “25th percentile”:
Definition 1: The nth percentile is the lowest score that is greater than a certain percentage (“n”) of the scores. In this example, our n is 25, so we’re looking for the lowest score that is greater than 25%.
Definition 2: The nth percentile is the smallest score that is greater than or equal to a certain percentage of the scores. To rephrase this, it’s the percentage of data that falls at or below a certain observation. This is the definition used in AP statistics. In this example, the 25th percentile is the score that’s greater or equal to 25% of the scores.
They may seem very similar, but they can lead to big differences in results, although they are both the 25th percentile rank. Take the following list of test scores, ordered by rank:
| Score | Rank |
|---|---|
| 30 | 1 |
| 33 | 2 |
| 43 | 3 |
| 53 | 4 |
| 56 | 5 |
| 67 | 6 |
| 68 | 7 |
| 72 | 8 |
3.
 How to Find a Percentile
How to Find a Percentile
Need help? Check out our tutoring page!
Example question: Find out where the 25th percentile is in the above list.
Step 1: Calculate what rank is at the 25th percentile. Use the following formula:
Rank = Percentile / 100 * (number of items + 1)
Rank = 25 / 100 * (8 + 1) = 0.25 * 9 = 2.25.
A rank of 2.25 is at the 25th percentile. However, there isn’t a rank of 2.25 (ever heard of a high school rank of 2.25? I haven’t!), so you must either round up, or round down. As 2.25 is closer to 2 than 3, I’m going to round down to a rank of 2.
Step 2: Choose either definition 1 or 2:
Definition 1: The lowest score that is greater than 25% of the scores. That equals a score of 43 on this list (a rank of 3).
Definition 2: The smallest score that is greater than or equal to 25% of the scores. That equals a score of 33 on this list (a rank of 2).
Depending on which definition you use, the 25th percentile could be reported at 33 or 43! A third definition attempts to correct this possible misinterpretation:
Definition 3: A weighted mean of the percentiles from the first two definitions.
In the above example, here’s how the percentile would be worked out using the weighted mean:
- Multiply the difference between the scores by 0.25 (the fraction of the rank we calculated above). The scores were 43 and 33, giving us a difference of 10:
(0.25)(43 – 33) = 2.5 - Add the result to the lower score. 2.5 + 33 = 35.5
In this case, the 25th percentile score is 35.5, which makes more sense as it’s in the middle of 43 and 33.
In most cases, the percentile is usually definition #1. However, it would be wise to double check that any statistics about percentiles are created using that first definition.
4. Percentile Range
A percentile range is the difference between two specified percentiles. these could theoretically be any two percentiles, but the 10-90 percentile range is the most common. To find the 10-90 percentile range:
these could theoretically be any two percentiles, but the 10-90 percentile range is the most common. To find the 10-90 percentile range:
- Calculate the 10th percentile using the above steps.
- Calculate the 90th percentile using the above steps.
- Subtract Step 1 (the 10th percentile) from Step 2 (the 90th percentile).
References
Kenney, J. F. and Keeping, E. S. “Percentile Ranks.” §3.6 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 38-39, 1962.
CITE THIS AS:
Stephanie Glen. "Percentiles, Percentile Rank & Percentile Range: Definition & Examples" From StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/probability-and-statistics/percentiles-rank-range/
Need help with a homework or test question? With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is free!
Your first 30 minutes with a Chegg tutor is free!
What Percentile Tells You about a Statistical Value
By: Deborah J. Rumsey and
Updated: 07-12-2021
From The Book: Statistics For Dummies
Statistics For Dummies
Explore Book Buy On Amazon
Percentiles report the relative standing of a particular value within a statistical data set. If that’s what you’re most interested in, the actual mean and standard deviation of the data set are not important, and neither is the actual data value. What’s important is where you stand — not in relation to the mean, but in relation to everyone else: That’s what a percentile gives you.For example, in the case of exam scores, who cares what the mean is, as long as you scored better than most of the class? Who knows, it may have been an impossible exam and 40 points out of 100 was a great score. In this case, your score itself is meaningless, but your percentile tells you everything.
In this case, your score itself is meaningless, but your percentile tells you everything.
Suppose your exam score is better than 90 percent of the rest of the class. That means your exam score is at the 90th percentile (so k = 90), which hopefully gets you an A. Conversely, if your score is at the 10th percentile (which would never happen to you, because you’re such an excellent student), then k = 10; that means only 10 percent of the other scores are below yours, and 90 percent of them are above yours; in this case an A is not in your future.
A nice property of percentiles is they have a universal interpretation: Being at the 95th percentile means the same thing no matter if you are looking at exam scores or weights of packages sent through the postal service; the 95th percentile always means 95 percent of the other values lie below yours, and 5 percent lie above it. This also allows you to fairly compare two data sets that have different means and standard deviations (like ACT scores in reading versus math). It evens the playing field and gives you a way to compare apples to oranges, so to speak.
It evens the playing field and gives you a way to compare apples to oranges, so to speak.
A percentile is not a percent; a percentile is a value (or the average of two values) in the data set that marks a certain percentage of the way through the data. Suppose your score on the GRE was reported to be the 80th percentile. This doesn’t mean you scored 80 percent of the questions correctly. It means that 80 percent of the students’ scores were lower than yours and 20 percent of the students’ scores were higher than yours.
This article is from the book:
- Statistics For Dummies ,
About the book author:
Deborah J. Rumsey, PhD, is an Auxiliary Professor and Statistics Education Specialist at The Ohio State University. She is the author of Statistics For Dummies, Statistics II For Dummies, Statistics Workbook For Dummies, and Probability For Dummies.
This article can be found in the category:
- Statistics ,
Use of percentile charts in myopia control
Axial length (AL) is perhaps the most important parameter on which to judge the progression of myopia. In the control of myopia, the AL value measured for a particular child and its change over the years are compared with the standard values obtained as average values for the population.
For this purpose, percentile charts are used, which present a set of curves for changing axial length with age for different percentiles (from 5th to 9th5th, step may be 5 or more). Percentiles reflect the prevalence of age-AL combination in a given population. So, if the AL value for a given age lies on the 10th percentile curve (on the 10th percentile), then this means that 10% of the population of this age have an axial length less than this AL value, and 90% more.
Axial length-age percentile charts (and corresponding tables) for European children can be taken, for example, from the article (https://bjo.bmj.com/content/early/2021/11/09/bjophthalmol-2021-319431), published in 2021 in the British Journal of Ophthalmology. Percentile curves are also used in the Myopia module of Haag-Streit's LENSTAR biometer.
Consider 2 examples of the use of percentiles in myopia control. For a 7-year-old Chinese girl, the measured AL was 22.40 mm (ref. error +1.50 D). This AL value for 7 years on the percentile chart (for the Chinese population) is at the 35th percentile. This means that 35 out of 100 girls at the age of 7 years have eyes less than 22.40 mm, and 65 out of 100 girls at the age of 7 have eyes longer than 22.40 mm. By the age of 8, the girl's eye grew to 22.64 mm (ref. error +0.75 D), the percentile remained the same (35th), which indicates a stable growth pattern. However, at 9years, AL increased to 23.15 mm (ref. error -0.50 D), which already corresponds to the 45th percentile. This indicates that the child's AL has shifted by 10 percentiles. A 10 percent increase may indicate an unusual increase in eye length between 8 and 9 years. An upward shift in percentiles indicates a higher risk of developing myopia, which warrants further evaluation and treatment if necessary.
This indicates that the child's AL has shifted by 10 percentiles. A 10 percent increase may indicate an unusual increase in eye length between 8 and 9 years. An upward shift in percentiles indicates a higher risk of developing myopia, which warrants further evaluation and treatment if necessary.
Consider the second example. A 9 year old European boy has a measured AL of 23.5 mm (ref. error -1.00 D). These values are in the 65th percentile, indicating that the boy's AL is greater than 65% of boys 9years. Considering this percentile, refractive status, and other risk factors, the use of myopia control methods was recommended. The AL values measured at 10 and 11 years old were 23.6 mm and 23.65 mm (ref. error in both cases -1.25 D). Although the AL increased, the percentile decreased to the 60th, indicating an improvement over both the baseline percentile and the population mean.
As these examples show, measured AL values and their percentiles indicate the location of a child's AL relative to population averages and can be used to control myopia. Measurement of AL and percentiles during follow-up of the child can help to observe the growth pattern of the eye and evaluate the effectiveness of the method of myopia control. nine0004
Measurement of AL and percentiles during follow-up of the child can help to observe the growth pattern of the eye and evaluate the effectiveness of the method of myopia control. nine0004
Adapted from publication (https://reviewofmm.com/listening-to-patients-needs-led-me-to-myopia-management/).
What is the percentile (percentile) of the journal Scopus
Scopus is a single abstract and bibliographic database that includes scientific literature. Scopus was created by the Elsevier publishing house, which provides access through a special institutional subscription.
Interest in this database is obvious and not accidental. For specialists who have a scientific degree, it is important to publish their scientific materials in the relevant publications that are in this database. But being in Scopus itself is not a sufficient condition for a scientific journal to be relevant for publication. The publication must have an appropriate rating in SiteScore and percentile.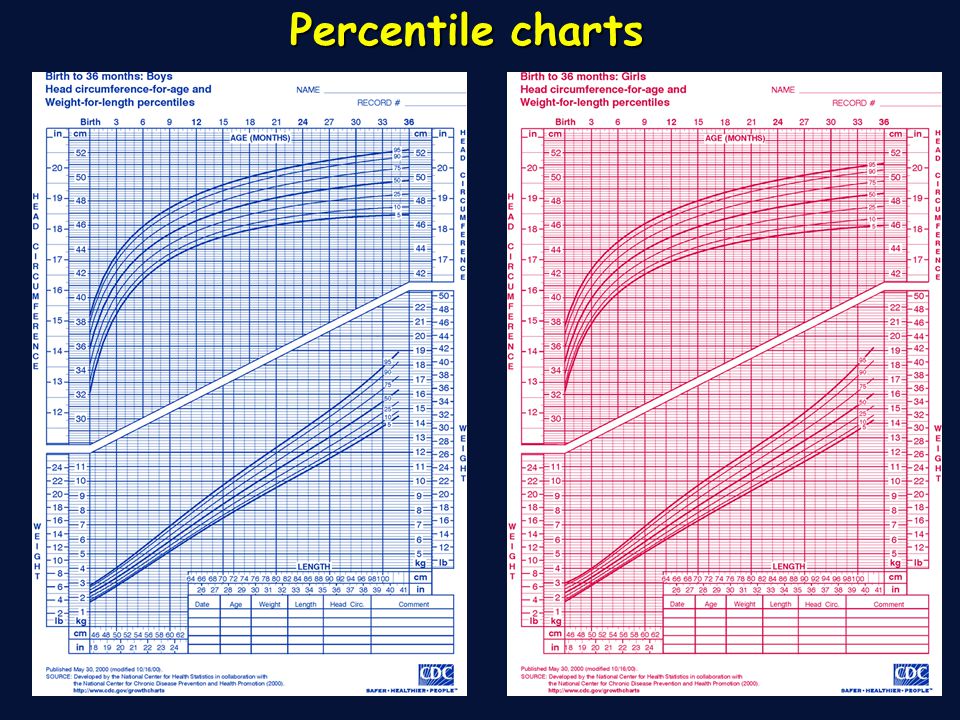 Otherwise, the article will not be taken into account. Therefore, it is very important to understand such indicators in order to be able to choose a publication for publishing your scientific materials as correctly as possible. nine0004
Otherwise, the article will not be taken into account. Therefore, it is very important to understand such indicators in order to be able to choose a publication for publishing your scientific materials as correctly as possible. nine0004
Percentiles and quartiles
First, let's consider the terminology in its basic sense, and then move specifically to the Scopus database and examples of analysis of the necessary indicators.
The term "percentile" refers to a measure in which the percentage of total values is equal to or less than the given measure. For example, 90 percent of the data values are below the 90 percentile. Or 10 percent of the data values are below the 10 percentile. As for quartiles, it means values that divide the data table into four parts. This is a general designation of concepts. And now let's consider it applicable to the Scopus database. nine0004
- 25% - Q1, 1st quartile, 99-75th percentile;
- 25% - Q2, II quartile, 74-50 percentiles;
- 25% - Q3, III quartile, 49-25 percentiles;
- 25% - Q4, IV quartile, 24-1 percentile.

If you take into account this scheme, then it is not so difficult to navigate the structure of the Scopus database. Next, let's move on to examples of how this looks in practice in a more detailed form. But first, let's look at another important issue.
In which case the 9 percentile is not calculated for the journal0024
Scopus percentile is not calculated in the following situations:
- when a scientific journal was accepted into Scopus earlier than 3 years ago. In this case, everything is quite understandable, since there is not enough data for the calculation;
- when a scientific journal was removed from Scopus.
In all other situations, such an indicator can be calculated without problems.
How to determine the quartile of a scientific journal by percentile
Although some of the definitions seem complicated at first glance, in practice they can be quite easily understood. Each subject category to which a particular scientific journal belongs has its own gradation. According to the AJSC classification, all journals within a category are ranked in descending CiteScore. Let's look at a specific example. Suppose we are dealing with the 86th percentile. This means that a scientific journal belongs to the 14% (from 100 you need to subtract 86) publications with the highest CiteScore in a particular field. nine0004
According to the AJSC classification, all journals within a category are ranked in descending CiteScore. Let's look at a specific example. Suppose we are dealing with the 86th percentile. This means that a scientific journal belongs to the 14% (from 100 you need to subtract 86) publications with the highest CiteScore in a particular field. nine0004
And, of course, this answer would be incomplete without considering what the CiteScore concept in Scopus is based around. In simple words, CiteScore is the rating that a scientific journal has in the Scopus database. The formation of this indicator takes into account how many documents were cited during the year (we are talking about documents that were published in the previous 3 years). This indicator is then divided by the number of documents that were indexed in Scopus and published during the same period. nine0004
By the way, there is another important aspect when a scientific journal is related to several areas in Scopus at once. In such cases, you can see that in each such area, the journal has a different percentile. Accordingly, the highest of them is selected. This will be the final percentile of a scientific journal in Scopus.
In such cases, you can see that in each such area, the journal has a different percentile. Accordingly, the highest of them is selected. This will be the final percentile of a scientific journal in Scopus.
Wrapping Up…
For all professionals who hold a degree or academic degree, understanding the information described in this article is essential to being able to use the Scopus database effectively. For each such expert in their field, it is important to have two scientific materials in the form of an article published in a peer-reviewed international scientific journal, which is in the Scopus database. But this is not the only requirement. The SiteScore percentile must be at least 35 in one of the scientific fields. nine0004
As for the military, specialists from higher military institutions, scientific organizations or special educational institutions, there is a slightly different requirement. There must be 3 scientific articles whose percentile in Scopus has a value of at least 50.