4 month percentile
Baby weight and height tracker growth chart
- Baby
- Baby Development
Tip: Track your child's growth over time by logging into your account.
New to BabyCenter? Join now
Child's name
Date of birth
Enter birthday
Sex
Boy Girl
Date of measurement
Enter date
Weight
lb.kg. oz.
Height
in.cm.
Head circumference
cm.in.
By Rebekah Wahlberg
|
|
June 21, 2022
Our growth percentile calculator shows how your baby's size compares with other boys or girls the same age. Just enter your child's weight, height (aka length), and head circumference, and we'll calculate a percentile for each. The number reflects what percentage of kids is larger or smaller than your baby. So if your 3-month-old baby is in the 40th percentile for weight, that means 40 percent of 3-month-old babies weigh less than your baby, and 60 percent weigh more.
Using our baby growth chart
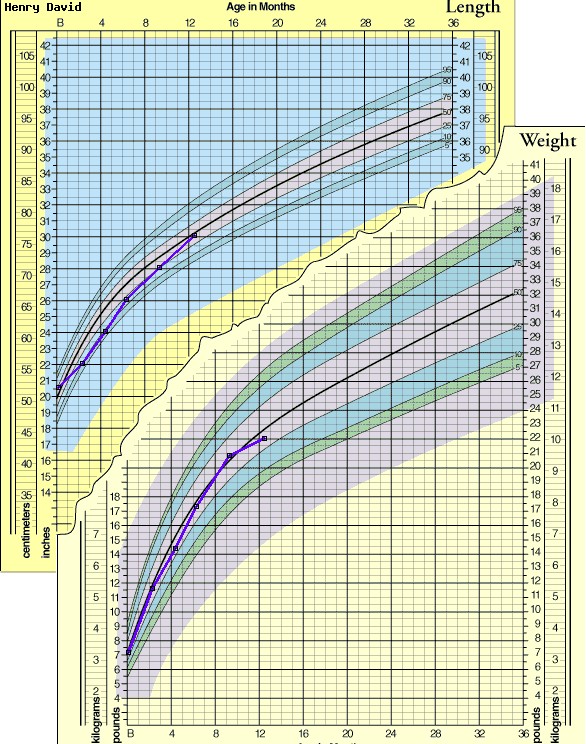
When your baby is first born, you'll have several visits at your pediatrician's office to make sure your baby's growth is on track. Your pediatrician will plot your baby's weight, height, and head circumference on a growth chart.
Don't be concerned if your baby doesn't fall right in the middle of the growth chart, though. There's a wide range of normal, and your baby's measurements now don't necessarily reflect what size they'll be as an adult. It's normal for some children to be in the 10th percentile for weight, while other children are in the 90th percentile. The most important thing is that your baby is growing at a healthy and consistent rate, no matter what percentile they're in.
Our growth percentile calculator is a general educational tool only.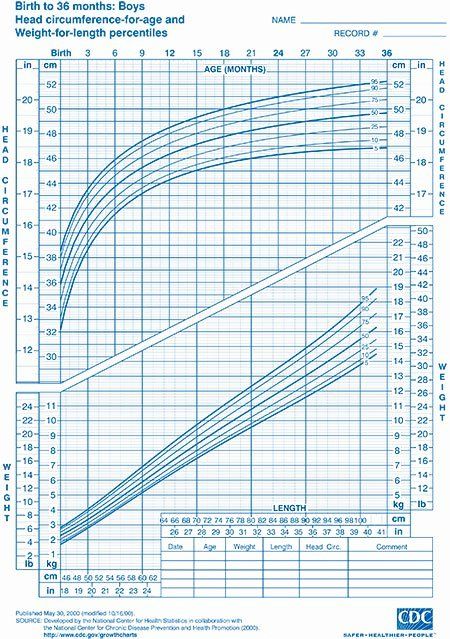 It's not the last word on how your child is growing, and it's not a substitute for having a healthcare provider monitor your child's growth at regularly scheduled exams. At these visits, your provider will determine whether your child is following a healthy growth pattern over time.
It's not the last word on how your child is growing, and it's not a substitute for having a healthcare provider monitor your child's growth at regularly scheduled exams. At these visits, your provider will determine whether your child is following a healthy growth pattern over time.
This tool is for children under age 2 and is based on World Health Organization data for kids in that age group. And if you'd like, you can find out how tall your older child is likely to be with our Child Height Predictor.
Read on to learn more about the measurements healthcare professionals take, and learn how to measure your baby at home.
Baby weight
If you want to see how your baby is growing between doctor visits, here's how to get a fairly accurate weight at home:
- Undress your baby completely (remove their diaper, too) and step on a scale while you're holding them. Record that weight.
- Then, set your baby down and weigh yourself. Subtract your own weight from your combined weight with your baby and record that number.
- This isn't as accurate as weighing your baby at the doctor's office, but it's a good estimate of how much your baby weighs.
- If you're worried about your baby's weight gain, call your baby's pediatrician. They may have you come in for a visit, since it's important to have your baby weighed on a consistent scale that can accurately measure weight in pounds and ounces.
Baby height
Before your baby can stand and walk on their own, their height is often recorded as their "length" – that is, how long they are from the crown of their head to the bottom of their heel while lying down. If you want to measure your baby's length at home between doctor visits, here's how:
- Lay your baby down on a flat surface and stretch a measuring tape from the top of their head to the bottom of their heel. Since babies' knees naturally bend a bit, you may need a second person to stretch out their legs while you take the measurement.
- Record their length to the nearest tenth of a centimeter or inch.
 (In the hospital, birth length is often recorded in centimeters, but your pediatrician's office will likely record their length in inches. What you do is up to you!) Your record might be a little different than the doctor's, but that's okay.
(In the hospital, birth length is often recorded in centimeters, but your pediatrician's office will likely record their length in inches. What you do is up to you!) Your record might be a little different than the doctor's, but that's okay.
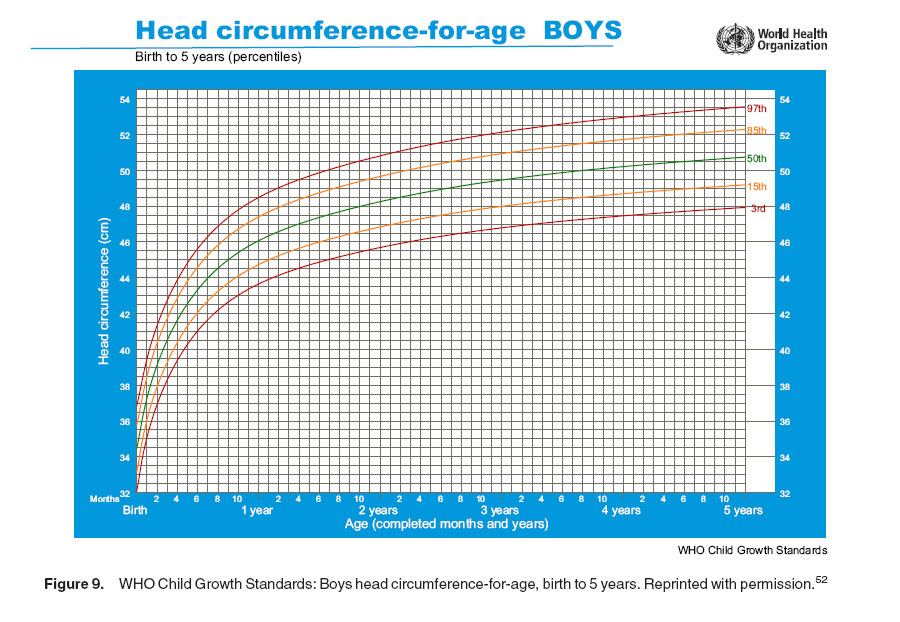
Baby head circumference
Your baby's healthcare provider will measure their head circumference for the first two years of their life to make sure your baby's brain is growing at a healthy rate.
You can measure your baby's head circumference at home, but it can be hard to do this accurately. Here's how to get a good estimate:
- Wrap a flexible measuring tape around the widest part of your baby's head, just above the eyebrows and ears and around the back where their head slopes out from their neck.
- Take the measurement three times (your baby may be wiggly, which could make getting an accurate measurement tough) and use the largest measurement to the nearest 0.1 centimeter.
Are you sure you want to delete this entry?
Yes Cancel
New entry
Edit entry
Your entry couldn't be saved.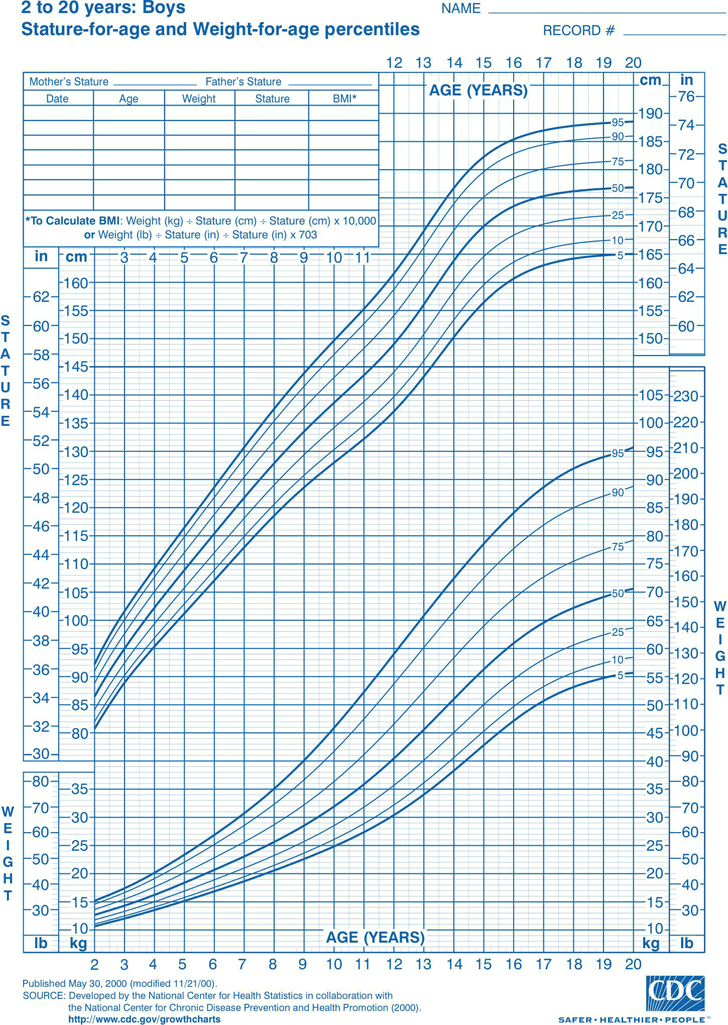 Please try again later.
Please try again later.
advertisement | page continues below
advertisement
Featured video
All pregnancy, parenting, and birth videos >
Get the BabyCenter app
The #1 app for tracking pregnancy and baby growth.
Download now
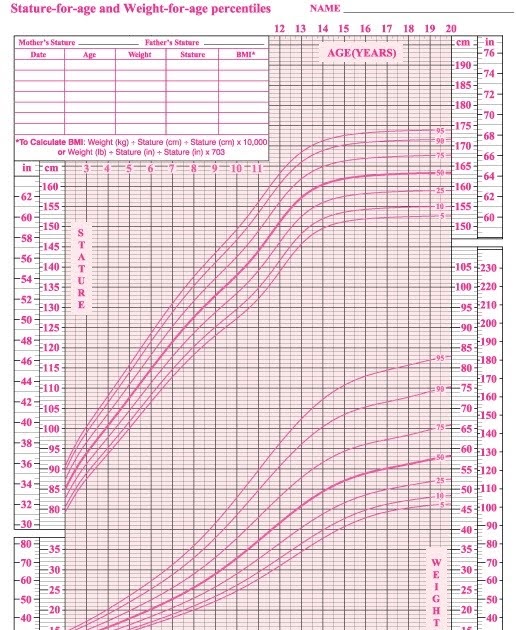
Growth Charts - Individual Growth Charts
- Set 1: Individual charts with all percentiles
- Set 2: Individual charts with 5th and 95th percentiles
- Set 3: Individual charts with 3rd and 97th percentiles
- Summary files
The individual growth charts, with one chart per page, have the grids aligned to English units (lb, in), with metric units (kg, cm) on the secondary scale. Individual charts are available for boys and for girls. The individual charts include the following:
Infants, birth to 36 months
- Weight-for-age
- Length-for-age
- Weight-for-length
- Head circumference-for-age
Children and adolescents, 2 to 20 years
- Weight-for-age
- Stature-for-age
- Body mass index-for-age
Preschoolers, 2 to 5 years
- Weight-for-stature
The individual growth charts were published in three sets.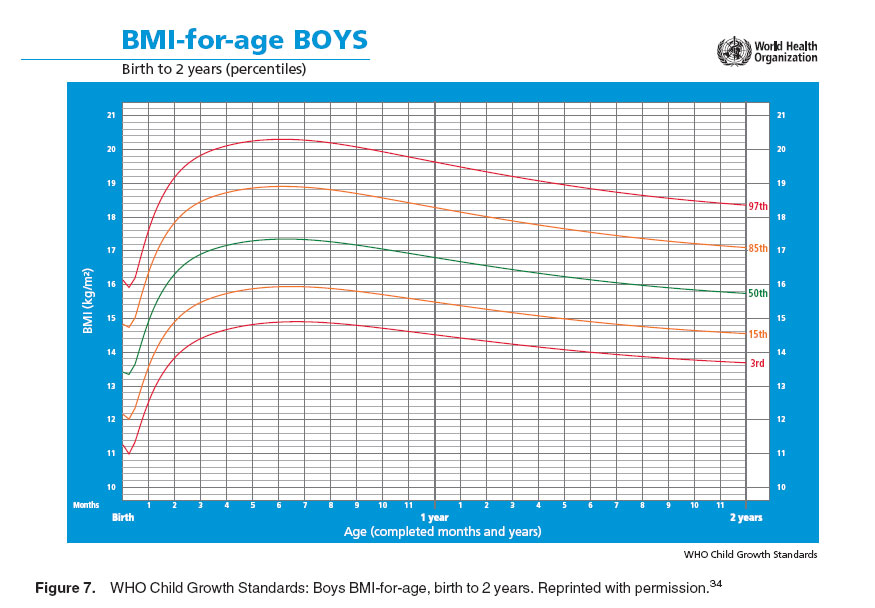
- Set 1 contains 16 charts (8 for boys and 8 for girls), with the 3rd, 5th, 10th, 25th, 50th, 75th, 90th ,95th, and 97th smoothed percentile lines for all charts, and the 85th percentile for BMI-for-age and weight-for-stature.
- Set 2 contains 16 charts (8 for boys and 8 for girls), with the 5th, 10th, 25th, 50th, 75th, 90th, and 95th smoothed percentile lines for all charts, and the 85th percentile for BMI-for-age and weight-for-stature.
- Set 3 contains 16 charts (8 for boys and 8 for girls), with the 3rd, 10th, 25th, 50th, 75th, 90th, and 97th smoothed percentile lines for all charts, and the 85th percentile for BMI-for-age and weight-for-stature.
These three distinct sets of charts are provided to meet the needs of various users. Set 1 shows all of the major percentile curves, but may have limitations where the curves are close together, especially at the youngest ages. Most users in the United States may wish to use the format shown in set 2 for the majority of routine applications.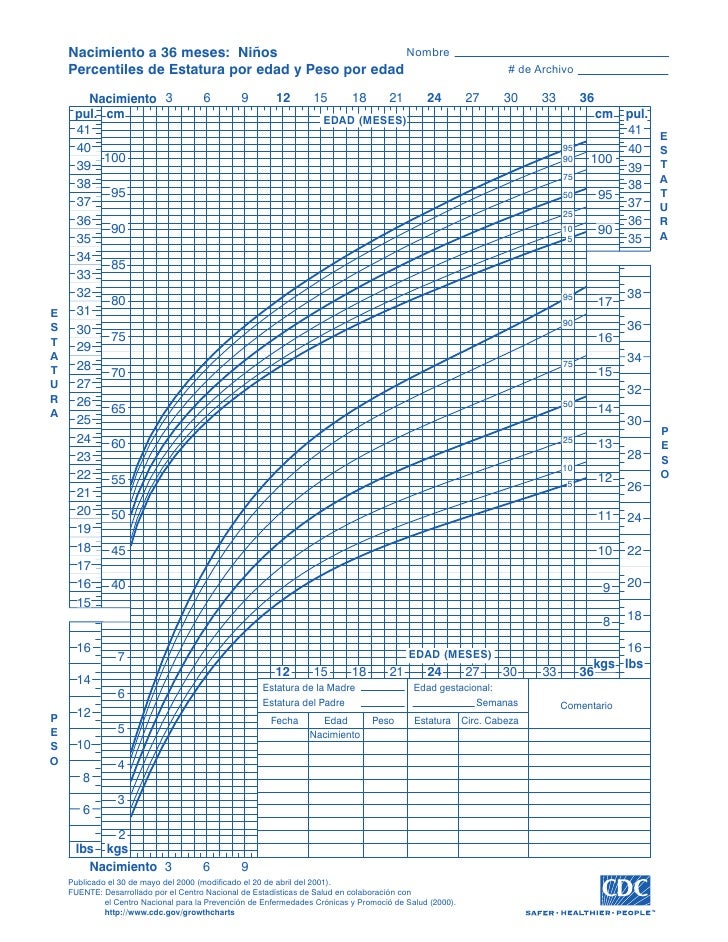 Pediatric endocrinologists and others dealing with special populations may wish to use the format in set 3 for selected applications.
Pediatric endocrinologists and others dealing with special populations may wish to use the format in set 3 for selected applications.
Within each set, individual charts can be accessed by pointing to the associated URL. In addition, all charts in each set are combined into 3 summary files. These summary files contain the individual charts from either set 1, set 2, or set 3, as described above.
All individual 2000 CDC growth charts have an initial publication date of May 30, 2000. For various reasons, selected charts were modified after the initial publication date. Modifications were made to selected individual charts to correct or enhance particular aspects of the graphs. Where applicable, when individual charts were further modified, the date is indicated on each chart. In all cases where individual charts were modified, the data points in the corresponding data file remain unchanged from the initial release on May 30, 2000. The individual growth charts for weight-for-length and weight-for-stature were modified because the smoothed percentile lines were incorrectly graphed on the grids that were initially published.
All individual growth charts may be viewed, downloaded, and printed in Adobe Acrobat. For routine viewing and printing, the individual charts are available as PDF (600 dpi screen optimized) files.
Suggested citation
Centers for Disease Control and Prevention, National Center for Health Statistics. CDC growth charts: United States.
http://www.cdc.gov/growthcharts/. May 30, 2000.
Set 1: Individual charts with all percentiles (3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th)
- Weight-for-age percentiles: Boys, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 45 KB]
- Weight-for-age percentiles: Girls, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 45 KB]
- Length-for-age percentiles: Boys, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 45 KB]
- Length-for-age percentiles: Girls, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 44 KB]
- Weight-for-length percentiles: Boys, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 48 KB]
Revised and corrected 6/8/00.
- Weight-for-length percentiles: Girls, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 48 KB]
Revised and corrected 6/8/00. - Head circumference-for-age percentiles: Boys, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 48 KB]
- Head circumference-for-age percentiles: Girls, birth to 36 months 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 48 KB]
- Weight-for-age percentiles: Boys, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 54 KB]
- Weight-for-age percentiles: Girls, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 53 KB]
- Stature-for-age percentiles: Boys, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 55 KB]
- Stature-for-age percentiles: Girls, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 54 KB]
- Weight-for-stature percentiles: Boys 3rd, 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 44 KB]
Revised and corrected 11/21/00.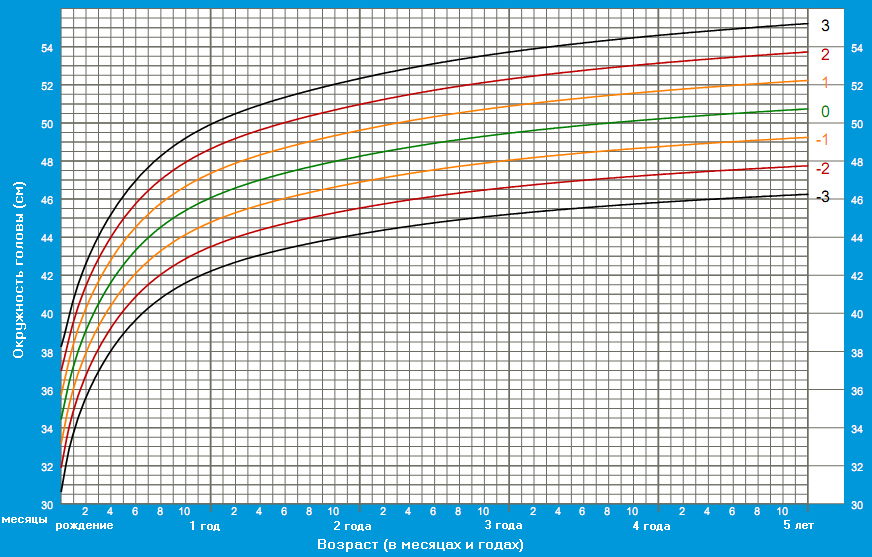
- Weight-for-stature percentiles: Girls 3rd, 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 44 KB]
Revised and corrected 11/21/00. - Body mass index-for-age percentiles: Boys, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 58 KB]
- Body mass index-for-age percentiles: Girls, 2 to 20 years 3rd, 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th, 97th percentiles Cdc-pdf[PDF – 58 KB] [PDF – 58 KB]
Set 2: Individual charts with 5th and 95th percentiles (5th, 10th, 25th, 50th, 75th, 90th, 95th)
- Weight-for-age percentiles: Boys, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 45K]
- Weight-for-age percentiles: Girls, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 45K]
- Length-for-age percentiles: Boys, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 45K]
- Length-for-age percentiles: Girls, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 45K]
- Weight-for-length percentiles: Boys, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 48K]
Revised and corrected 6/8/00.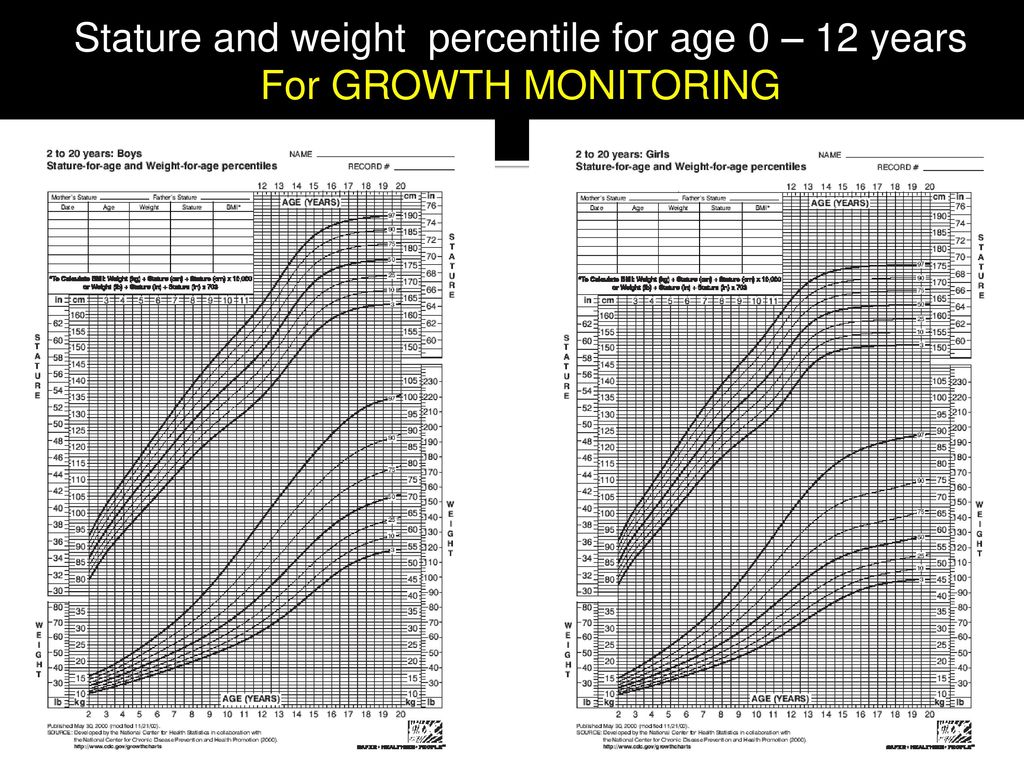
- Weight-for-length percentiles: Girls, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 48K]
Revised and corrected 6/8/00. - Head circumference-for-age percentiles: Boys, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 48K]
- Head circumference-for-age percentiles: Girls, birth to 36 months 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 48K]
- Weight-for-age percentiles: Boys, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 52K]
- Weight-for-age percentiles: Girls, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 52K]
- Stature-for-age percentiles: Boys, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 53K]
- Stature-for-age percentiles: Girls, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Cdc-pdf[PDF – 52K]
- Weight-for-stature percentiles: Boys 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th percentiles Cdc-pdf[PDF – 44K]
Revised and corrected 11/21/00.
- Weight-for-stature percentiles: Girls 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th percentiles Cdc-pdf[PDF – 44K]
Revised and corrected 11/21/00. - Body mass index-for-age percentiles: Boys, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th percentiles Cdc-pdf[PDF – 56K]
- Body mass index-for-age percentiles: Girls, 2 to 20 years 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th percentiles Cdc-pdf[PDF – 56K]
Set 3: Individual charts with 3rd and 97th percentiles (3rd, 10th, 25th, 50th, 75th, 90th, 97th)
- Weight-for-age percentiles: Boys, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 45K]
- Weight-for-age percentiles: Girls, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 45K]
- Length-for-age percentiles: Boys, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 45K]
- Length-for-age percentiles: Girls, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 45K]
- Weight-for-length percentiles: Boys, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 48K]
Revised and corrected 6/8/00.
- Weight-for-length percentiles: Girls, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 48K]
Revised and corrected 6/8/00. - Head circumference-for-age percentiles: Boys, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 48K]
- Head circumference-for-age percentiles: Girls, birth to 36 months 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 48K]
- Weight-for-age percentiles: Boys, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 52K]
- Weight-for-age percentiles: Girls, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 52K]
- Stature-for-age percentiles: Boys, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 53K]
- Stature-for-age percentiles: Girls, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Cdc-pdf[PDF – 52K]
- Weight-for-stature percentiles: Boys 3rd, 10th, 25th, 50th, 75th, 85th, 90th, 97th percentiles Cdc-pdf[PDF – 44K]
Revised and corrected 11/21/00.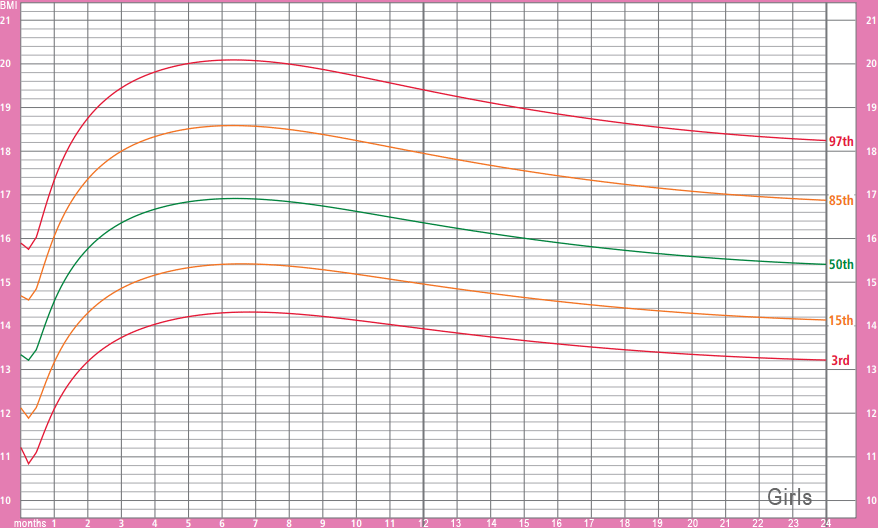
- Weight-for-stature percentiles: Girls 3rd, 10th, 25th, 50th, 75th, 85th, 90th, 97th percentiles Cdc-pdf[PDF – 44K]
Revised and corrected 11/21/00. - Body mass index-for-age percentiles: Boys, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 85th, 90th, 97th percentiles Cdc-pdf[PDF – 56K]
- Body mass index-for-age percentiles: Girls, 2 to 20 years 3rd, 10th, 25th, 50th, 75th, 85th, 90th, 97th percentiles Cdc-pdf[PDF – 56K]
Summary Files
- Set 1 summary file; 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97th percentiles Download all 16 charts in Set 1 Cdc-pdf[PDF – 556 KB]
Revised and corrected 6/8/00 and 11/21/00. - Set 2 summary file; 5th, 10th, 25th, 50th, 75th, 90th, 95th percentiles Download all 16 charts in Set 2 Cdc-pdf[PDF – 538 KB]
Revised and corrected 6/8/00 and 11/21/00. - Set 3 summary file; 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles Download all 16 charts in Set 3 Cdc-pdf[PDF – 539 KB]
Revised and corrected 6/8/00 and 11/21/00.
| Random converter |
Percentile calculatorThis calculator determines P th percentile for the original dataset. Example: calculate the 95th percentile for the following dataset: 3.77; 3.96; 4.26; 3.99; 3.79; 3.90; 4.30; 4.28; 4.16; 4.13; 4.03; 4.55; 4.56; 4.64; 4.85; 4.69; 4.47; 4.99; 5.14; 4.68; 4.91; 5.03; 4.71; 4.57; 4.94; 4.96; 4.97; 5.25; 4.72; 5.06; 4.78; 4.36; 5.00; 4.87; 4.53; 4.06; 4.00; 4.39. Data set Enter numbers separated by “ ; ". Maximum number of characters: 1000 percentile P % 0 ≤ P ≤ 100 Share Share a link to this calculator, including input parameters Twitter FaceBook 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 Definition 1Definition 2 Definition 3 Enter the data set and percentile and click the Calculate button. Description and examplesPercentile (also called percentile, percentile and centile in different sources and versions of programs) is a statistical measure that indicates the value that a given random variable does not exceed with a specified probability. For example, the phrase "95th percentile is 7" means that 95% of all measured values do not reach the value of 7 and only 5% of all measured values exceed this value. When a service provider for placing client equipment in a data center, connecting it to power supply and communication channels (colocation) issues a monthly invoice for payment of services based on 95th percentile (English bustable billing), which means that the provider cuts off 5% of peak traffic values per month. This calculation method allows users to have short periods of very high traffic, perhaps dozens of times higher than "regular" traffic, at no extra charge. If billed monthly, then users can have very high traffic (within the allocated bandwidth) for 24 × 30 × 0. Percentiles are also often used by pediatricians to estimate children's height compared to World Health Organization (WHO) statistics for weight, height and head circumference. The percentile value allows you to compare the head circumference, weight and height of the child with the data of other children. For example, the 60th percentile of height means that the girl is taller than 60% of other girls and shorter than 40% of other girls. Definitions It is interesting to note that although we often use percentiles, there is no universal definition for this term. Here we will give three percentile definitions, one simple and two not so simple, since they use linear interpolation. Other definitions of percentile can be found in the literature. Calculations by all definitions give similar results if the number of values in the observational data is large. If the number of values is small, then the results can be quite different. Definition 1According to the first definition, the P th percentile of a list of N numbers ordered by magnitude (from smallest to largest) is the smallest number in the list that is greater than N percent of all numbers of the series under study. For example, in the children's height example above, the 60th percentile means a height that is greater than the height of 60% of other children. This definition uses the nearest rank method. Note that any value calculated by this method will always be present in the original data set. To calculate the percentile, you need to arrange the values in the data set in order from smallest to largest and assign 9 to each value in the data set0024 serial number (rank) . Then the sequence number n is calculated for the given percentile using the formula:
The notation ⌈x⌉ means that the result is rounded up to the nearest whole number. This rounding is also called the ceiling. The 100th percentile is defined as the largest value in the original data set. Definition 2This and the following definitions use linear interpolation between adjacent values in the data set to improve accuracy. This is done instead of rounding to an integer value according to the first definition. There are several variants of this method. Here we will consider only two of them, which are used in MS Excel, starting from version 2010, and in some other programs. The fractional ordinal x is calculated using the following formula:
In versions of Excel older than 2010, this formula is used in the PERCENTILE.INC() function (English version), which is called PERCENTILE.INC() in the Russian version. This is a function that returns results for the entire range of values 0 ≤ P ≤ 1. To obtain the serial number n , the result of the calculation according to the above formula is rounded down to the nearest whole number down, that is, to a number that does not exceed the rounded value. For example, the results 2.2 and 2.7 will be rounded up to the ordinal of the value from the input dataset n = 2. The fractional part { x } of the result of calculating the fractional ordinal x is then used to further calculate the percentile value v by two adjacent values from the original data set: values with the calculated sequence number v n and the next higher value v n+1 :
where by definition is the fractional partBelow is an example of the calculation for definition 2. definition 3According to this definition, to calculate the fractional serial number x , a different formula is used than that used for definition 2:
In versions of Excel older than 2010, this formula is used in the PERCENTILE. As in definition 2, the result is rounded down to the nearest whole number, that is, to a number that does not exceed the rounded value. For example, the results 2.2 and 2.7 will be rounded up to the ordinal value from the input dataset n = 2. As in definition 2, the fractional part { x } of the result of calculating the fractional ordinal x is then also used to further calculate the percentile value v for two adjacent values from the original data set: the value with the calculated sequence number v n and the next higher value v n+1 :
where by definition of the fractional part
Examples of calculating percentiles the methods described above. The values in the dataset are ordered from smallest to largest, and each is assigned a rank from 1 to 12. We will run a calculation on the three definitions and compare the results of our calculations. 9 The values in the dataset are ordered from smallest to largest, and each is assigned a rank from 1 to 12. We will run a calculation on the three definitions and compare the results of our calculations. 9 | |
| 24 | 10 | |
| 29 | ||
Calculation according to method 1
Determined order wound N by determination of 1 for 40 percentage :
Since the ordinal rank n is not an integer, we round it up to n = 5. From Table 1, the 40th percentile value for n = 5 is 11.
Calculation according to method 2
This method is an alternative to the nearest rank method. It uses linear interpolation between adjacent values in the dataset. Fractional rank x is calculated using the following formula:
Rank n = 5 percentile v for two adjacent values from the original data set: values with the calculated sequence number v n and the next higher value v n+1 :
Calculation by this method08
is another alternative to the nearest rank method.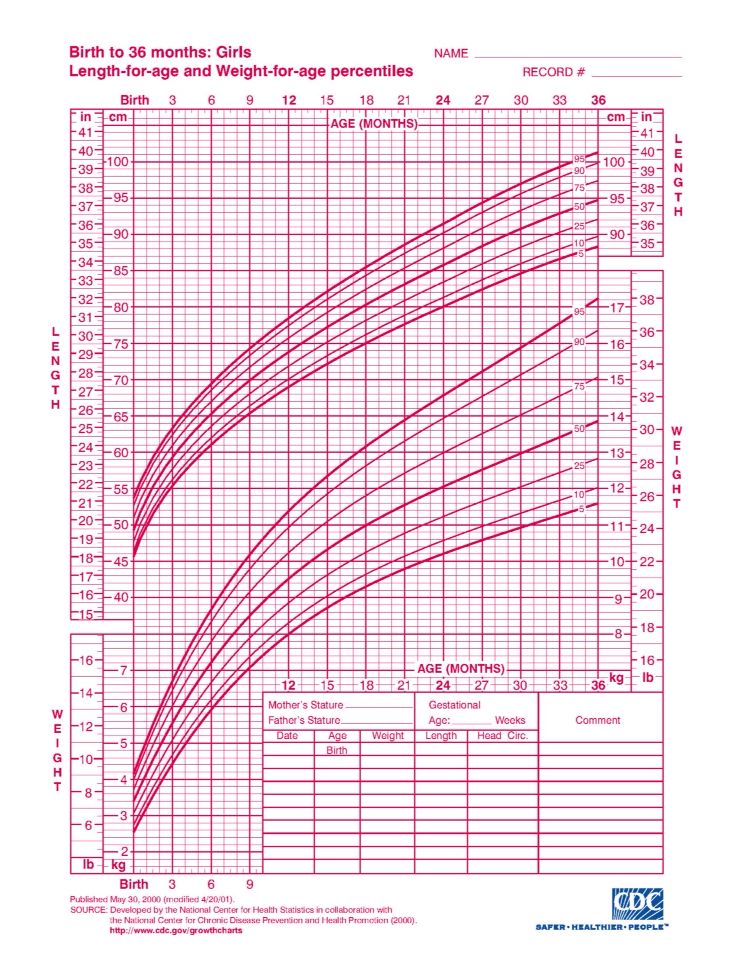 It uses linear interpolation between adjacent values in the dataset. Determine the fractional serial number x :
It uses linear interpolation between adjacent values in the dataset. Determine the fractional serial number x :
Ordinal rank n = 5. The fractional part { x } = 0.2 of the result of calculating the fractional ordinal x is then used to further calculate the percentile value v for two adjacent values from the original dataset: values with the calculated ordinal v n followed by a higher value v n+1 :
View these examples in a calculator.
Payment method by 9The 5th percentile is the industry standard method for measuring bandwidth (bandwidth) of a link used by ISPs and data centers.
Using percentiles
95th percentile billing method
95th percentile billing method is an industry standard method for measuring bandwidth (capacity) of a channel used by ISPs and data centers. The method allows users to dramatically increase traffic for 5% of the time without increasing the cost of paying for data center services. The method is based on peak load accounting and is commonly used for billing traffic for equipment installed in data centers.
The method is based on peak load accounting and is commonly used for billing traffic for equipment installed in data centers.
This graph shows the ISP channel load statistics measured over 32 hours.
1. Average outgoing traffic 2.9 megabits per second (Mbps).
2. 95th percentile outbound 4.1 Mbps.
3. Maximum outgoing traffic 5.7 Mbps.
4. Filtered traffic peaks are not taken into account in the billing calculation.
Because the 95th percentile is 4.1 Mbps, in this example the ISP is billing 5 Mbps because it has a 1 Mbps increment. This should be taken into account when determining the cost of services. If 9The 5th percentile was 3.9 Mbps, this ISP would have billed 4 Mbps.
Most ISPs use a five-minute sampling interval to record traffic and then calculate usage at the 95th percentile. Sometimes providers offer a 90th percentile calculation in order to attract more customers. The average channel width during the sampling interval represents the value of the data set, which is calculated as the number of megabits transmitted through the communication port divided by the length of the five-minute sampling interval (300 seconds).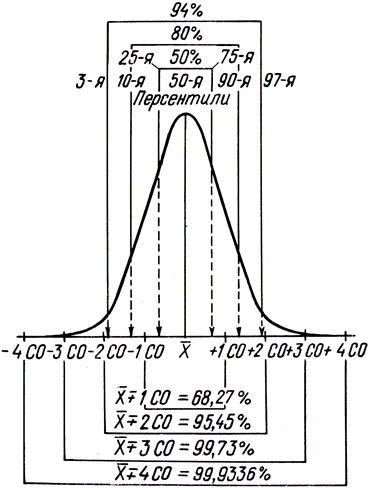 During the monthly period for which the customer is billed, there will be about 9 such values in the calculation datasetthousand. This data set is then sorted as described above and the top 5% of the data with the most traffic is discarded. The value of the 95th percentile is indicated on the invoice, but only if it exceeds the guaranteed bandwidth of the channel specified in the contract and paid by the client in any case, even if the real traffic is less than this bandwidth, since the guaranteed bandwidth is usually included in the cost of operating a rented or own server in the data center.
During the monthly period for which the customer is billed, there will be about 9 such values in the calculation datasetthousand. This data set is then sorted as described above and the top 5% of the data with the most traffic is discarded. The value of the 95th percentile is indicated on the invoice, but only if it exceeds the guaranteed bandwidth of the channel specified in the contract and paid by the client in any case, even if the real traffic is less than this bandwidth, since the guaranteed bandwidth is usually included in the cost of operating a rented or own server in the data center.
Based on this model, high traffic for 24 hours × 30 days × 0.05 = 36 hours is not included in the monthly bill. To determine the 95th percentile, it is common to consider both outgoing and incoming traffic.
Data center customers who pay for its services at the 95th percentile can pay per megabit of regularly used bandwidth and at the same time, if necessary, can dramatically increase traffic for short periods of time without financial consequences.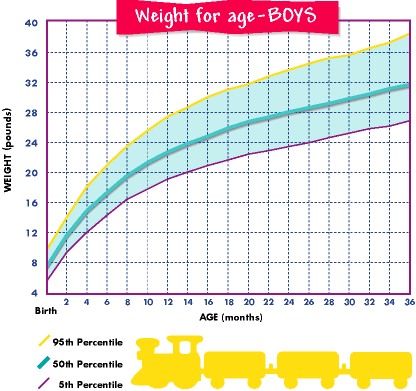
In this monthly traffic example, the data center customer pays for the 95th percentile, which is only about 4.5 Mbps. At the same time, the peak traffic is 95 Mbps and it is not taken into account when calculating the payment, since these periods are short.
Child body mass index, weight and height
Body mass index (BMI) is defined as the ratio of body mass in kilograms to the square of height in meters and is usually expressed in kg/m² even in the few countries where traditional units of measurement are still used . The body mass index characterizes people into groups of underweight (up to 18.5 kg/m²), normal weight (8.5–25 kg/m²), overweight (25–30 kg/m²), and obesity (over 30 kg/m²).
Children with a weight between the 5th and 85th percentile are classified as normal weight
In children and adolescents, body mass index is defined differently. The calculation uses the same formula as for adults, but the categorization is different: instead of being compared to several fixed thresholds (underweight, normal weight, overweight, and obese), BMI is compared to the percentile value for children of the same sex, age and living in the same country.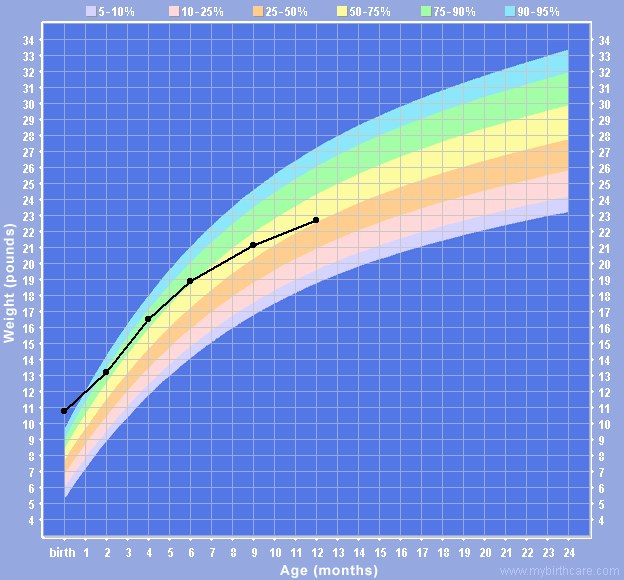 For example, the phrase “a girl has a body mass index of the 40th percentile” means that 40% of girls of the same age have a lower body mass index. Children with a BMI below the 5th percentile are considered to be underweight for their age, while those with a BMI between the 5th and 85th percentile are considered to be of normal body weight. Those with a BMI between 85 and 9The 4th percentile is considered overweight and over the 94th percentile is considered obese.
For example, the phrase “a girl has a body mass index of the 40th percentile” means that 40% of girls of the same age have a lower body mass index. Children with a BMI below the 5th percentile are considered to be underweight for their age, while those with a BMI between the 5th and 85th percentile are considered to be of normal body weight. Those with a BMI between 85 and 9The 4th percentile is considered overweight and over the 94th percentile is considered obese.
Pediatrics often use the weight and height of a child to assess their physical development compared to growth charts that show the averages and percentiles for children of different ages and sex for a given country.
Of course, body mass index can hardly be called an ideal indicator. It does not take into account many factors of physical development, such as the mass of adipose tissue and muscles and body type. BMI may misinterpret an athlete with a large muscle mass as overweight and at the same time not note the disadvantage of a person with excessive body fat mass, who, despite a normal body mass index, belongs to a group of people with an increased risk of cardiovascular diseases, diabetes type 2 and premature death.
Percentile scores in education
Another common example in Western education is percentile test scores, which are the percentage of performance below a given target. Test scores in the form of percentiles can often be found in the reports that schools provide to parents. For example, if a student ranks in the 60th percentile, this means that the student did better than 60% of the other students. In other words, this result is better than the average and means that the student studied well. Percentile results for students or students who take a test or exam allow you to compare the performance of an individual student with other students in the comparison group.
Test results in percentile form can often be found in the reports that schools provide to parents.
Author of the article: Anatoly Zolotkov
You may be interested in other calculators from the Mathematics group:
Distance calculator between two points
Circle length and circle area 9000 Calculator Complex numbers
9000Delayed physical development of the child - symptoms, treatment in Zheleznodorozhny
13. 03.2017
03.2017
Physical retardation is a significant lag of the child according to anthropometric criteria from their peers. Often this condition is characterized by a delay in the development of motor abilities and cognitive skills.
Anthropometric data (height, weight, chest circumference, head circumference, etc.) are assessed using centile tables compiled specifically for children of different ages and genders. If the anthropometric data of a child go beyond the 3rd-5th centile, or for a short period of time there has been a significant decrease in them (for example, from a level of more than the 75th percentile to a level less than the 25th), we can talk about a delay in physical development. There is a traditional distinction between physical developmental delay due to the presence of diseases (organic) and physical developmental delay associated with psychological and social factors (psychosocial, inorganic), observed in children under the age of five.
Symptoms of delayed physical development of the child
The severity of manifestations can range from a slight delay in growth and body weight, to severe manifestations, including loss of the subcutaneous fat layer, reduction in muscle mass, dermatitis, hair loss, the development of recurrent infections.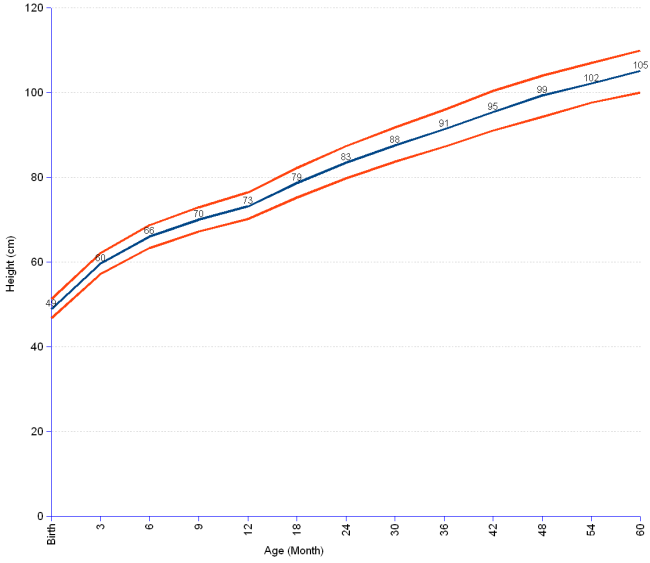 In the most severe cases, protein-energy (marasmus) or protein depletion (kwashiorkor) develops. Delayed physical development in developed countries is most often characterized by minimal impairments diagnosed in a polyclinic setting. In developing countries, more severe manifestations requiring inpatient treatment are more common.
In the most severe cases, protein-energy (marasmus) or protein depletion (kwashiorkor) develops. Delayed physical development in developed countries is most often characterized by minimal impairments diagnosed in a polyclinic setting. In developing countries, more severe manifestations requiring inpatient treatment are more common.
The degree of delay can be set for each anthropometric parameter (height, body weight, weight-height index) as a percentage of the average statistical age standards. In the presence of concomitant diseases, it is necessary to repeatedly determine anthropometric parameters in dynamics. In the case of premature babies, the degree of prematurity is also taken into account, since up to one or two years old, when comparing anthropometric data, it is necessary to adjust the age.
Lagging can be characterized as mild, moderate or severe with body weight equal to 75-90, 60-74 and less than 60% of the due, height - 90-95, 85-89 and less than 85% of the due, weight-height index - 81 -90, 70-80 and less than 70% of the due.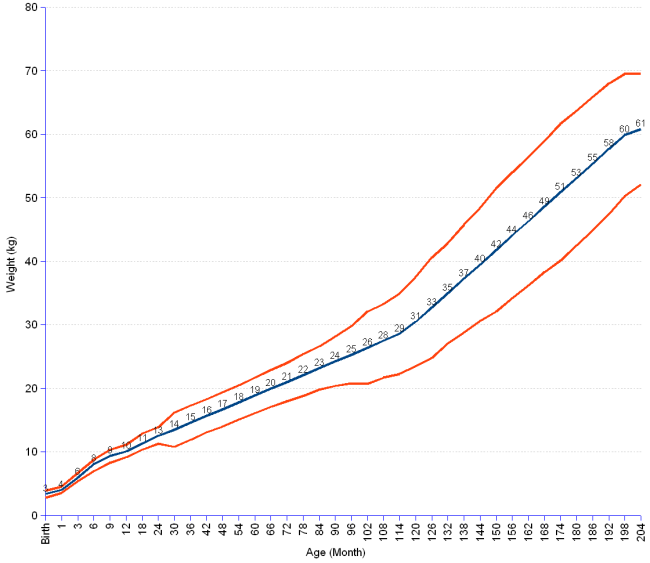 The lag in mass usually outstrips the lag in growth. In chronic malnutrition, there is a synchronous growth retardation and weight gain.
The lag in mass usually outstrips the lag in growth. In chronic malnutrition, there is a synchronous growth retardation and weight gain.
If physical development is delayed, laboratory examination is usually not very informative, therefore it is recommended to limit yourself to the most basic analyzes. These include general clinical tests of blood, urine, and blood. It is important to assess the bone age of the child. For this, an x-ray of the hands is performed with the capture of l / carpal joints. The presence of ossification points (nuclei) is analyzed. Bone age can correspond to the passport age, lag behind it or get ahead of it. Thanks to this study, it is possible to identify family short stature, in which the bone age corresponds to the passport one, to suggest the presence of endocrine diseases or dietary abnormalities, which makes it possible to determine the range of further examination.
Treatment of delayed physical development of a child
When making a diagnosis, it is necessary to take into account the anamnesis and clinical manifestations, as well as assess the relationship between the child and his parents, which plays an important role. For successful treatment, a thorough assessment of the child's nutritional characteristics, identification of social problems, economic difficulties, and conflict situations in the family is required. It is necessary to promote the formation of a favorable atmosphere in the family, the preparation of a proper diet. With an organic delay in physical development, an important role is played by the correctly selected therapy of the underlying disease. Features of nutrition are determined by the severity of the delay in physical development, as well as the nature of the underlying disease.
For successful treatment, a thorough assessment of the child's nutritional characteristics, identification of social problems, economic difficulties, and conflict situations in the family is required. It is necessary to promote the formation of a favorable atmosphere in the family, the preparation of a proper diet. With an organic delay in physical development, an important role is played by the correctly selected therapy of the underlying disease. Features of nutrition are determined by the severity of the delay in physical development, as well as the nature of the underlying disease.
Hospitalization is carried out in case of a pronounced delay in physical development, in case of exhaustion, the need for examination, and also when there are suspicions of the inadequacy of the attitude of parents towards their child. If the reason for the delay is a disease, a selection of therapy is carried out in the hospital.
By contacting our CMC, you can be sure of professional and high-quality assistance from our leading specialists.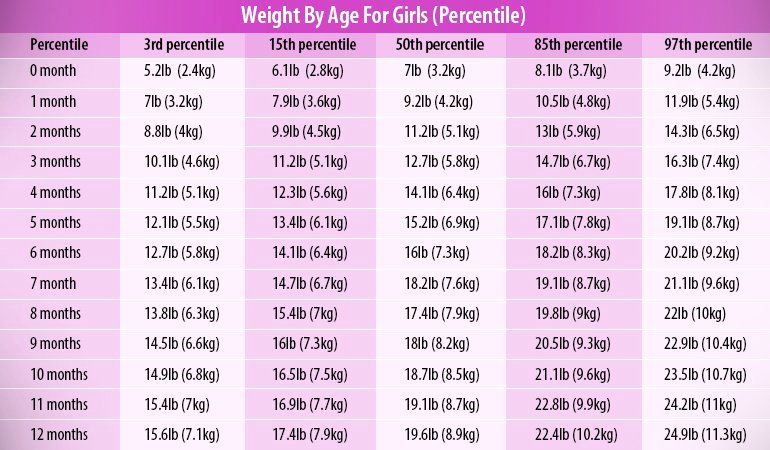

 05 = 36 hours at no additional charge. An example of such traffic is shown in the figure below.
05 = 36 hours at no additional charge. An example of such traffic is shown in the figure below. 
 For example, results of 2.2 and 2.7 will be rounded up to 3. After that, the percentile value v is taken from the values sorted in order by ordinal number n .
For example, results of 2.2 and 2.7 will be rounded up to 3. After that, the percentile value v is taken from the values sorted in order by ordinal number n . 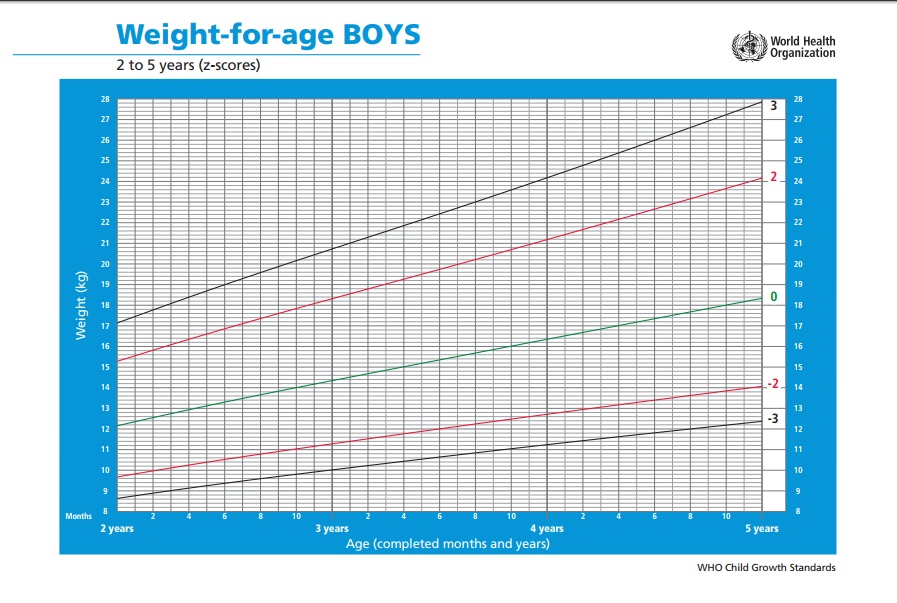 If P = 1, PERCENTILE.INC() returns the highest value of the dataset, and if P = 0, then PERCENTILE.INC() returns the low value of the dataset.
If P = 1, PERCENTILE.INC() returns the highest value of the dataset, and if P = 0, then PERCENTILE.INC() returns the low value of the dataset. 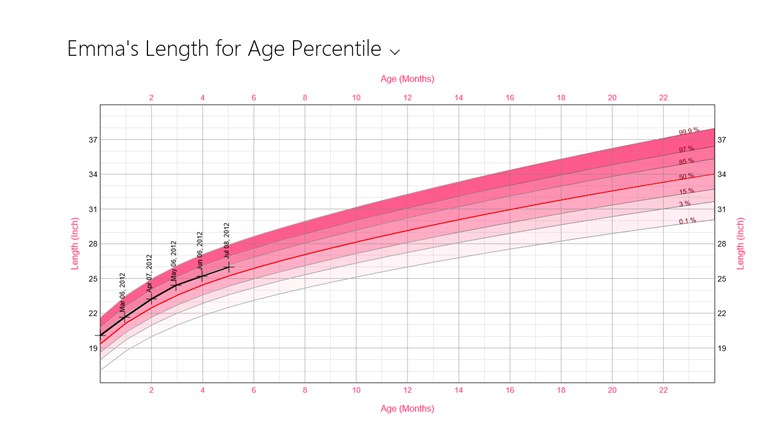 EXC() (English version) and PERCENTILE.EXC() (Russian version) functions. This function throws an error if P is outside the valid range for the given source data set. This means that PERCENTILE.EXC() only interpolates if the value of the specified percentile is between two values in the original dataset. If the function cannot interpolate, it returns an error. For example, if the dataset contains 10 values, you cannot get a result for a percentile value less than 10% and greater than 90%. At the same time, the PERCENTILE.INC() function, by its second definition, will produce a valid result in this situation.
EXC() (English version) and PERCENTILE.EXC() (Russian version) functions. This function throws an error if P is outside the valid range for the given source data set. This means that PERCENTILE.EXC() only interpolates if the value of the specified percentile is between two values in the original dataset. If the function cannot interpolate, it returns an error. For example, if the dataset contains 10 values, you cannot get a result for a percentile value less than 10% and greater than 90%. At the same time, the PERCENTILE.INC() function, by its second definition, will produce a valid result in this situation.